CommonRoad Raceline Planner
The CommonRoad Raceline Planner combines several algorithms for raceline global trajectory planning for autonomous racing. Our work is based on code of the Indy Racing Team at TU Munich [1,2], namely the groups from Prof. Betz (AVS) and Prof. Lienkamp (FTM) and the following papers [3-6]. This toolbox is a collaboration between TUM CPS, AVS and FTM.
Featured Planners
Currently, the toolbox features the following planners: - shortest path planner: plans the shortest path using convex optimization - minimum curvature planner: plans the path with minimum curvature
Example
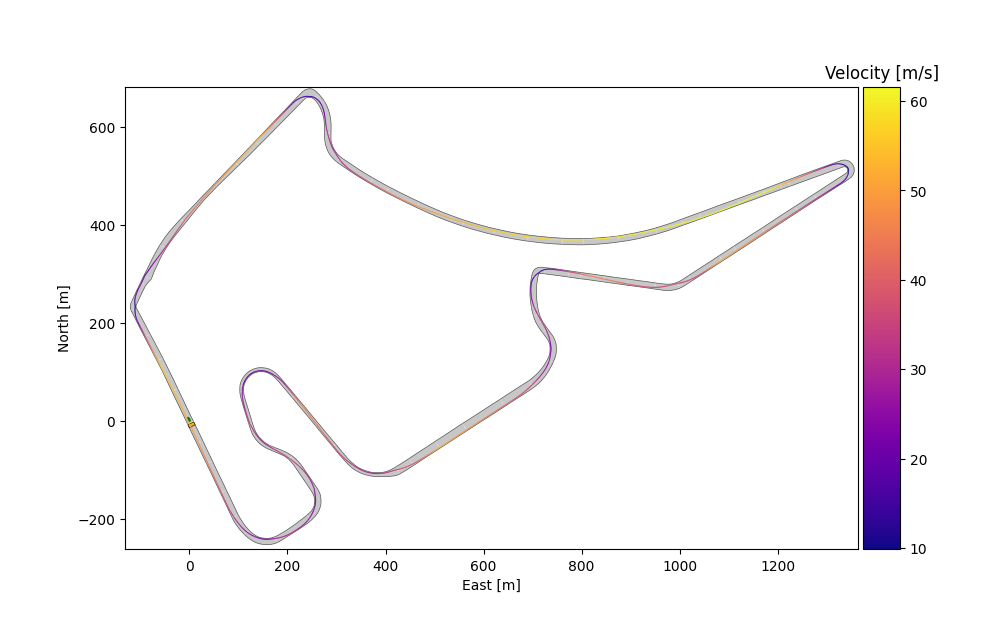
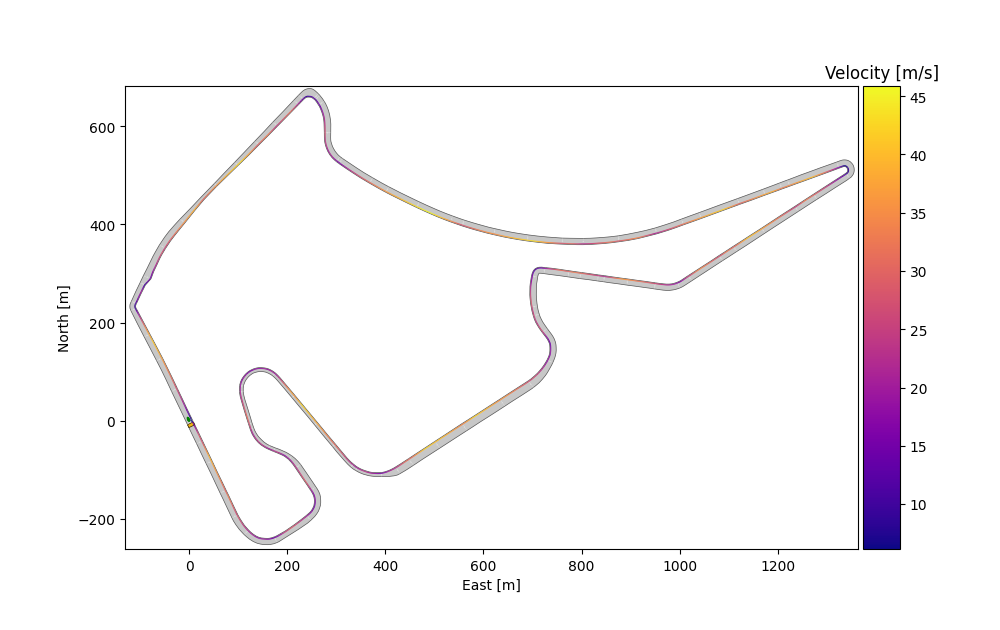
Depcited is the Formula 1 racing track Hockenheimring in Germany. The color coding is always relative to the minimum and maximum values in the current velocity profile in m/s.
Formula 1 Hockenheim Ring
Minimum Curvature
Shortest Path
References
- [1] AVS and FTM (2024): TUMFTM/global_racetrajectory_optimization. Available online at: https://github.com/TUMFTM/global_racetrajectory_optimization
- [2] AVS and FTM (2024): TUMFTM/trajectory_planning_helpers. Available online at: https://github.com/TUMFTM/trajectory_planning_helpers
- [3] Heilmeier, A., Wischnewski, A., Hermansdorfer, L., Betz, J., Lienkamp, M., & Lohmann, B. (2020). Minimum curvature trajectory planning and control for an autonomous race car. Vehicle System Dynamics.
- [4] Betz, J., Wischnewski, A., Heilmeier, A., Nobis, F., Hermansdorfer, L., Stahl, T., ... & Lienkamp, M. (2019, November). A software architecture for the dynamic path planning of an autonomous racecar at the limits of handling. In 2019 IEEE international conference on connected vehicles and expo (ICCVE) (pp. 1-8). IEEE.
- [5] Betz, J., Betz, T., Fent, F., Geisslinger, M., Heilmeier, A., Hermansdorfer, L., ... & Wischnewski, A. (2023). Tum autonomous motorsport: An autonomous racing software for the indy autonomous challenge. Journal of Field Robotics, 40(4), 783-809.
- [6] E. Velenis and P. Tsiotras, "Optimal velocity profile generation for given acceleration limits: Theoretical analysis". In Proceedings of the 2005, American Control Conference, 2005, (pp. 1478-1483).
Authors
- Tobias Mascetta: tobias.mascetta[at]tum.de,
- Mohammed Aziz Bouziri: aziz.bouziri1[at]gmail.com
- Johannes Betz: betz[at]tum.de
- Based on and using code of: Alexander Heilmeier, Leonhard Hermannsdorfer, Fabian Christ, Tim Stahl, Boris Lohmann and Markus Lienkamp